Count Submatrices With All Ones Solution - Leetcode

Understand Leetcode Count Submatrices With All Ones(1504) With Brute Force and Optimal Solution

12 July 2020

This document presents the solution to the problem 1504 - Count Submatrices With All Ones - Leetcode.

Note: Make sure to go through the code comments as well. It’ll help you understand the concept better.

		
				
Given a rows * columns matrix mat of ones and zeros, return how many submatrices have all ones.

Example 1:

Input: mat = [[1,0,1],
              [1,1,0],
              [1,1,0]]
Output: 13
Explanation:
There are 6 rectangles of side 1x1.
There are 2 rectangles of side 1x2.
There are 3 rectangles of side 2x1.
There is 1 rectangle of side 2x2. 
There is 1 rectangle of side 3x1.
Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.

Example 2:

Input: mat = [[0,1,1,0],
              [0,1,1,1],
              [1,1,1,0]]
Output: 24
Explanation:
There are 8 rectangles of side 1x1.
There are 5 rectangles of side 1x2.
There are 2 rectangles of side 1x3. 
There are 4 rectangles of side 2x1.
There are 2 rectangles of side 2x2. 
There are 2 rectangles of side 3x1. 
There is 1 rectangle of side 3x2. 
Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.

Example 3:

Input: mat = [[1,1,1,1,1,1]]
Output: 21

Example 4:

Input: mat = [[1,0,1],[0,1,0],[1,0,1]]
Output: 5

Let’s start with a brute force approach for the input

input =  [][]int{
		{1, 0, 1},
		{1, 1, 0},
		{1, 1, 0},
	}

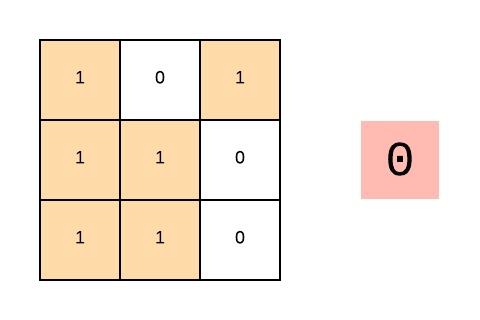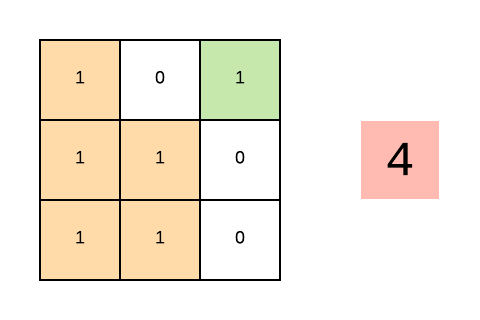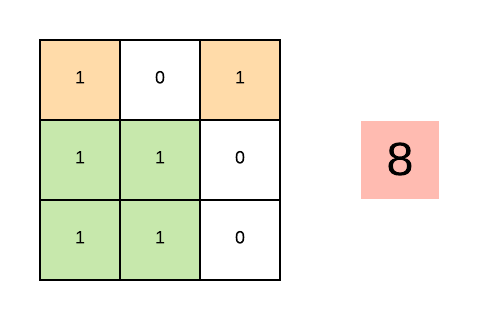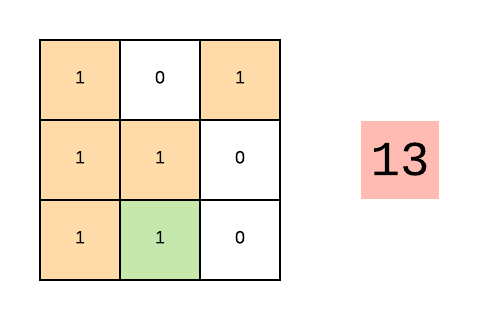
This animation shows the count of all the submatrices with all 1s on the right-hand side. The green areas show the found submatrices. The color changes to red if we encounter 0.

So, What would we be doing in a brute force approach? We’ll

Start with the first element of the array

Find the width of the continuous 1s on the right side from the current index.

input =  [][]int{
        {1, 0, 1},
        {1, 1, 0},
        {1, 1, 0},
    }

For [1][0], it is 2, containing [1][0] and [1][1] and for [0][0] it is only 1.
Keep the value of width inside maxWidth.
This will give the maximum width possible from the current index. Also, add 1 to numberOfSubMatrices if 1 is found.
Move to the next row at the same column and then count the number of continuous 1s, horizontally, from that index until maxWidth number of 1s are found.

If there are lesser 1s than maxWidth then replace the value of maxWidth with number of 1s found.

input =  [][]int{
        {1, 1, 1},
        {1, 1, 0},
        {1, 0, 0},
        {0, 0, 0},
    }

For this(^) example, maxWidth will be 3 for [0][0]. Then we’ll move to [1][0] and maxWidth will reduce to 2 and then to 1 and 0 subsequently while moving to the next row. Also, add 1 to numberOfSubMatrices if 1 is found.
Repeat this process until maxWidth is 0.
This way we’ve found all the submatrices starting at [0][0].
Repeat the steps 1 - 9 for all the indices in the input 2D array.

So, What will be the time complexity for this approach?

The steps 1-9 is of O(M*N) time complexity, and these steps are to be repeated on all the elements. This will make the time complexity O(M*N*M*N). If the input is a square matrix then the Time Complexity will be O(n^4).

What are the improvements that can be make on this approach?

In the steps 6-8, we’re horizontally looping over the row elements until the maxWidth number of 1s have been counted. If we know the maxWidth for all the indices beforehand then we won’t have to do steps 6-8.

This is how I’ve created the cache of maxWidth and maxHeight. The variable, depthWidthCache, contains the maxHeight and maxWidth for each of the element of the matrix on the same indices. For example, maxheight for [0][0] is stored at depthWidthCache[0][0][0] and maxWidth is stored at depthWidthCache[0][0][1].

func numSubmat(mat [][]int) int {
	numberOfSubMats := 0
	var depthWidthCache = make([][][2]int, len(mat))
	for i, matRow := range mat {
		depthWidthCache[i] = make([][2]int, len(matRow))
	}

    // calculating the maxWidth here
	for i := 0; i < len(mat); i++ {
		totalWidth := 0
		for j := len(mat[i]) - 1; j > -1; j-- {
			if mat[i][j] == 1 {
				totalWidth++
				depthWidthCache[i][j][1] = totalWidth
			} else {
				totalWidth = 0
			}
		}
	}

    // // calculating the maxHeight here  
    for j := 0; j < len(mat[0]); j++ {
        totalHeight := 0
        for i := len(mat) - 1; i > -1; i-- {
            if mat[i][j] == 1 {
                totalHeight++
                depthWidthCache[i][j][0] = totalHeight
            } else {
                totalHeight = 0
            }
        }
    }

For the following input:

[1, 0, 1]
[1, 1, 0]
[1, 1, 0]

depthWidthCache will be

[[3 1] [0 0] [1 1]]
[[2 2] [2 1] [0 0]]
[[1 2] [1 1] [0 0]]

[3 1] is the first element of depthWidthCache. It means that the element, mat[0][0] is part of a 3 x 1 matrix. Since, it is 3 x 1 matrix, it will also be a 2 x 1 and 1 x 1 as well with all of them starting at [0][0]. So, we’ll add 3 to numberOfSubMatrices.

Let’s take one more example:

[1 2] located at [2][0]. It means that the element, mat[2][0], is part of a 1 x 2 matrix. Since, it is 1 x 2 matrix, it will also be a 1 x 1 as well with all of them starting at [2][0]. So, we’ll add 2 to numberOfSubMatrices.

At [1][0] we find [2 2]. It mean that the maximum width from here is 2 and the maximum height from here is 2 as well. But, it doesn’t mean that there’s a matrix of 2 x 2 starting from here. It just tells the max height and max width from here is 2.

So, if the max width is 2 then it means that first row will contain 2 1s, i.e., [1][0] and [1][1]. We have to check whether the next maxHeight - 1 rows also contain the two 1s(or not?). If not, then we’ll reduce the maxWidth just like step 6.

Now, we can proceed with the actual solution:

numberOfSubMats := 0
for i := 0; i < len(mat); i++ {
    for j := 0; j < len(mat[0]); j++ {
    	currentDepth := depthWidthCache[i][j][0]
    	currentWidth := depthWidthCache[i][j][1]
    	if currentDepth == 0 && currentWidth == 0 {
            // if the current element is 0 then don't proceed
            // and don't increase the count as well
            continue
    	} else if currentDepth == 1 || currentWidth == 1 {
            if currentDepth == 1 && currentWidth == 1 {
                // this section means that we've found a 1
                // but it doesn't have any neighbour that is also 1
                numberOfSubMats++
            } else {
                // this section checks for the 1D matrix
                if currentDepth == 1 {
                    // add the width
                    numberOfSubMats += currentWidth
                } else {
                    // otherwise, add the height
                    numberOfSubMats += currentDepth
                }
            }
    	} else {
            numberOfSubMats += currentWidth
            for k := i + 1; k <= i+currentDepth-1; k++ {
    	        maxWidthFromNextRowElem := depthWidthCache[k][j][1]
    	        if maxWidthFromNextRowElem >= currentWidth {
                    numberOfSubMats += currentWidth
    	        } else {
                    numberOfSubMats += maxWidthFromNextRowElem
                    currentWidth = maxWidthFromNextRowElem
    	        }
            }
    	}
    }
}

Loading Comments... Disqus Loader

Count Submatrices With All Ones Solution - Leetcode

Understand Leetcode Count Submatrices With All Ones(1504) With Brute Force and Optimal Solution

Related Pages: