Codiwan.com

The blog for Design Patterns, Linux, HA and Myself!

Minimum Cost for Tickets Solution - Leetcode

Understand Leetcode Minimum Cost for Tickets With Brute Force and Optimal Solution

leetcode

dp

dynamic-programming

24 May 2020

This document presents the solution to the problem Minimum Cost For Tickets - Leetcode.

Note: Make sure to go through the code comments as well. It’ll help you understand the concept better.

Train on the Mountain 
		
				
In a country popular for train travel, you have planned some train travelling one year in advance. 
The days of the year that you will travel is given as an array days.  Each day is an integer from 1
to 365.

Train tickets are sold in 3 different ways:

    a 1-day pass is sold for costs[0] dollars;
    a 7-day pass is sold for costs[1] dollars;
    a 30-day pass is sold for costs[2] dollars.

The passes allow that many days of consecutive travel.  For example, if we get a 7-day pass on day 
2, then we can travel for 7 days: day 2, 3, 4, 5, 6, 7, and 8.

Return the minimum number of dollars you need to travel every day in the given list of days.

I’ll first try solving it by a brute force approach then I’ll move to a more optimal solution. While approaching towards the optimal solution, I’ll provide the approach behind the optimal solution.

Let’s start with the very first input:

Input: days = [1,4,6,7,8,20], costs = [2,7,15]

The days variable contains the exact 6 days on which a user can travel and, the cost variable contains the cost of 1 day, 7 day and 30 day tickets respectively.

Now, let’s proceed to solve it in a brute force way.

One the 1st day, the user can buy the 1day ticket, and it will be valid for that day only, or the user can buy the 7day ticket that will remain valid until 7th, or they can buy the 30day ticket thus making themselves able to travel on all days because the ticket will remain valid until 20th.

So, which ticket the user should buy?

They can buy 1day ticket on all the days, making the total cost = 12(6 * 2).

They can also buy one 7day ticket on 1st and then one 1day ticket on 8th and 20th, which makes the total cost = 11(7 + 2+ 2)

Or, they can buy the 30day ticket on 1st which will remain valid for all the days in this array. Here cost = 15

You might have observed that they are multiple choices the user can make on each of the day, however, they have to make sure the total amount spent remains minimum. For this example, the best solution is to buy one 7day ticket and two 1day tickets on 8 and 11.

What I’ll do in the brute force approach is to allow the user to buy all the types of tickets whenever they can and keep a cost of tickets. Once they reach the last day of the travel, I’ll compare their cost with the minimum cost. The minimum cost will be updated with current cost if that is lower.

For the input:

Input: days = [1,4,6,7,8,20], costs = [2,7,15]

This our flow diagram:

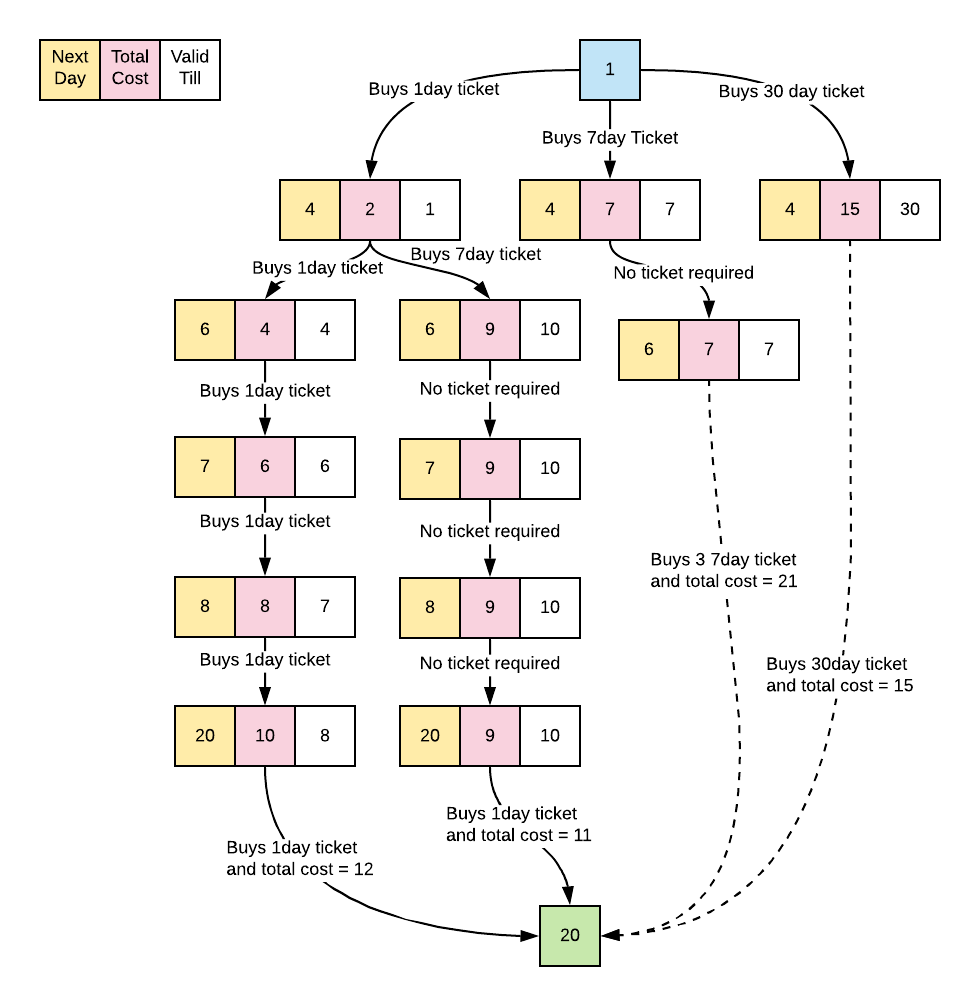
Minimum Cost for Tickets - Brute Force

In this diagram, you can see that on the first day the user had the choice to buy all the tickets so all the three tickets were bought and then based on the choices available they move ahead and finally travel the last day.

On the last day, the costs from all the choices are available, and the decision can be made to select the last one.

This is the code that I’ve written for brute force:

// mincostTickerBruteForce is called to get the solution.
func mincostTickerBruteForce(days []int, costs []int) int {
	return mincostNextDay(0, 0, 0, days, costs)
}

// mincostNextDay is called by mincostTickerBruteForce and then it calls itself recursively.
// Each successive recursion is the for proceeding to the next day after one of the ticket 
// is bought.
func mincostNextDay(currentDayIndex, validTill, totalCost int, days, cost []int) int {
	currentDay := days[currentDayIndex]
	if currentDayIndex == len(days)-1 {
        // this block is executed if the current day is the last day
		if currentDay <= validTill {
            // the final cost will be the totalCost if the ticket for
            // the current day was bought earlier
			return totalCost
		} else {
            // this block is executed if the user needs to buy the ticket 
			// for the last day
            // here we pick the smallest between 
            // cost[0], cost[1] and cost[2]
            // and add it to the totalCost
			nextCostToPick := 0
			if cost[0] <= cost[1] && cost[0] <= cost[2] {
				nextCostToPick = cost[0]
			} else if cost[1] <= cost[0] && cost[1] <= cost[2] {
				nextCostToPick = cost[1]
			} else {
				nextCostToPick = cost[2]
			}
			return totalCost + nextCostToPick
		}
	}
	minCost := math.MaxInt32
	if currentDay <= validTill {
        // this if block is executed if there is no need to buy a ticket for current day
        // as it was already purchased earlier using a 7day or a 30day ticket.
		minCost = mincostNextDay(currentDayIndex+1, validTill, totalCost, days, cost)
	} else {
        // this block is executed if the user has to buy the ticket for the current day

        // in this section user buys the ticket for the current day
		newCost := totalCost + cost[0]
        // the ticket is valid till current day as the ticket is bought only for the 
        // current day
		newValidTill := currentDay
        // proceed to the next day
		minCost = mincostNextDay(currentDayIndex+1, newValidTill, newCost, days, cost)

        // in this section user buys the ticket for the next 7 days
		newCost = totalCost + cost[1]
		// as the ticket is a 7day ticket, it remains valid for the next 6 days
		newValidTill = currentDay + 6
		thisCost := mincostNextDay(currentDayIndex+1, newValidTill, newCost, days, cost)
		if thisCost < minCost {
			minCost = thisCost
		}

        // here the 30day ticket is bought
		newCost = totalCost + cost[2]
		newValidTill = currentDay + 29
		thisCost = mincostNextDay(currentDayIndex+1, newValidTill, newCost, days, cost)
		if thisCost < minCost {
			minCost = thisCost
		}
	}
	return minCost
}

That was out brute force approach. If you find that I can be improved further then please provide your feedback in the comment section below.

Bored Passengers

We can, definitely, work on an optimal solution here because there will be Stackoverflow error if the input size is big.

Let’s proceed to solve this question in new way using the brute force approach that we’ve just created.

We’ll be using this matrix to solve our question from now on:

days/cost 1 4 6 7 8 20
2
7
15
Min Cost

The first row contains all the days on which the user has to travel, and the first column cost for 1day, 7day and 30day. The last row will contain the minimum cost for travelling on the nth day.

So, let’s buy the tickets for the 1st day:

days/cost 1 4 6 7 8 20
2 2
7 7 7 7 7
15 15 15 15 15 15 15
Min Cost 2 7 7 7 15 15

In the last row I’ve added the minimum cost for travelling for each of the days.

Now, let’s buy the tickets for the 4th day:

days/cost 1 4 6 7 8 20
2 2 4
7 7 7 7 7 9
15 15 15 15 15 15 15
Min Cost 2 4 7 7 9 15

The total cost until 1st day has been 2 dollars. Now,

The minimum cost for travelling on the 4th day is 4 dollars.

Now, let’s buy the tickets for the 6th day:

days/cost 1 4 6 7 8 20
2 2 4 6
7 7 7 7 7 9
15 15 15 15 15 15 15
Min Cost 2 4 6 7 9 15

The minimum cost for travelling on the 6th day is 6 dollars.

Now, the tickets for the 7th day:

days/cost 1 4 6 7 8 20
2 2 4 6 8
7 7 7 7 7 9
15 15 15 15 15 15 15
Min Cost 2 4 7 7 9 15

The user can buy a 1day ticket on the 8th day and then the cost will be 8(2 + 6) dollars, but they can already travel on the 8th day with 7 dollars.

Now, the tickets for the 8th day:

days/cost 1 4 6 7 8 20
2 2 4 6 8 9
7 7 7 7 7 9
15 15 15 15 15 15 15
Min Cost 2 4 7 7 9 15

Finally, for the 20th day

days/cost 1 4 6 7 8 20
2 2 4 6 8 9 11
7 7 7 7 7 9
15 15 15 15 15 15 15
Min Cost 2 4 7 7 9 15

This is how we’ll be solving this problem, by solving it for each of the days, i.e., Dynamic Programming.

I’m adding the code for the solution here. What I’ll do is:

func mincostTickets(days []int, costs []int) int {
	minTicketCost := make([]int, len(days))
	for i := range minTicketCost {
        // initialize all the elements with max int32 so that it will always be greater
        // than the values that we'll encounter
		minTicketCost[i] = math.MaxInt32
	}
	prevDayMinCost := 0
	for i := 0; i < len(days); i++ {
        // buy 1day ticket
		nextCost1 := prevDayMinCost + costs[0]
		
        // buy 7day ticket
        nextCost7 := prevDayMinCost + costs[1]
		// update the cost for next 7 days
        for j := i + 1; j < len(days); j++ {
			if days[j] > days[i]+6 {
				break
			}
			if minTicketCost[j] > nextCost7 {
				minTicketCost[j] = nextCost7
			}
		}

        // buy 7day ticket
		nextCost30 := prevDayMinCost + costs[2]
		// update the cost for next 30 days
        for j := i + 1; j < len(days); j++ {
			if days[j] > days[i]+29 {
				break
			}
			if minTicketCost[j] > nextCost30 {
				minTicketCost[j] = nextCost30
			}
		}
    
        // the min cost is found here for the current day
		if nextCost1 <= nextCost7 && nextCost1 <= nextCost30 {
			prevDayMinCost = nextCost1
		} else if nextCost7 <= nextCost1 && nextCost7 <= nextCost30 {
			prevDayMinCost = nextCost7
		} else {
			prevDayMinCost = nextCost30
		}
    
        // if the min cost is lower then we update the array, minTicketCost
		if prevDayMinCost < minTicketCost[i] {
			minTicketCost[i] = prevDayMinCost
		} else {
			prevDayMinCost = minTicketCost[i]
		}
		fmt.Println(minTicketCost)
	}

	return prevDayMinCost
}
Loading Comments... Disqus Loader
comments powered by Disqus

Related Pages: