Longest Arithmetic Sequence Solution - Leetcode
Leetcode Solution: Understand Leetcode problem Longest Arithmetic Sequence With a Brute Force and Optimal Solution
This document presents the solution to the problem 1027. Longest Arithmetic Sequence. We’ll look into the step by step approach to solve the problem and come up with the optimized way to solve this problem. This problem is similar to Arithemtic Slices Solution because in that problem we create continuous sequences having the same difference between the elements but in this problem, we’ve to find the non-continuous sequences as well.
Given an array A of integers, return the length of the longest arithmetic subsequence in A.
Recall that a subsequence of A is a list A[i_1], A[i_2], ..., A[i_k] with 0 <= i_1 < i_2 < ... < i_k <= A.length - 1,
and that a sequence B is arithmetic if B[i+1] - B[i] are all the same value (for 0 <= i < B.length - 1).
Example 1:
Input: [3,6,9,12]
Output: 4
Explanation: The whole array is an arithmetic sequence with steps of length = 3.
Example 2:
Input: [9,4,7,2,10]
Output: 3
Explanation:
The longest arithmetic subsequence is [4,7,10].
Example 3:
Input: [20,1,15,3,10,5,8]
Output: 4
Explanation:
The longest arithmetic subsequence is [20,15,10,5].
Note:
2 <= A.length <= 2000
0 <= A[i] <= 10000
Let’s start with an input that we’ll use for the solving this problem:
input := []int {
9, 4, 7, 2, 10, 13
}
Let us try to solve this problem in a brute force way. What I’ll do here is I’ll create a list of differences of all the elements with the current element and store it in the following format:
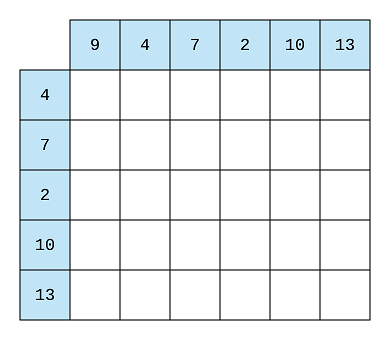
For example, for the 1st element, 9, the first column is storing all the differences, -5, -2, -7, 1, 4.
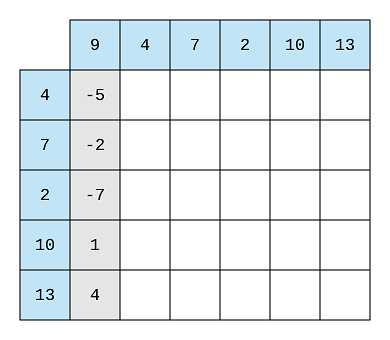
This way we can calculate all the differences. You’ll notice that the top right diagonal is blank because the differences
are always calculated for the elements appearing after the current element. Like, We will calculate the difference for 4
with 7, 2, 10, 13 only.
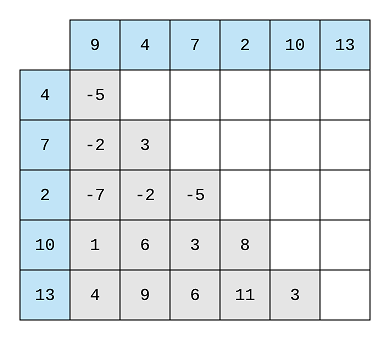
Now, the differences are calculated, we’ll loop through all the differences for each of the elements and try to find whether the same difference are present in the next element or not. This is the second step of the brute force approach. For example, 9 has a difference of -5 with 4. So, to grow the sequence we’ll have to check if 4 has a difference of -5 wih any subsequent element or not.
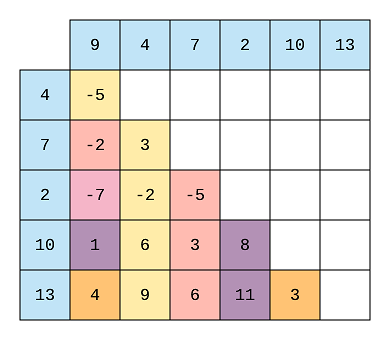
As 4 does not have any difference of -5 with any element after it, we move to the next difference -2 (7 - 9). Like 4, we don’t find -2 in the 3rd column, i.e, we can’t find any element present after 7 that will have a difference of -2 with 7. You’ll notice that there aren’t any difference in the first column that repeats for the subsequent elements.
The first difference we find here is 3(7 - 4). Now we have to check whether 3 is there in the 7’s or 3rd column or not.
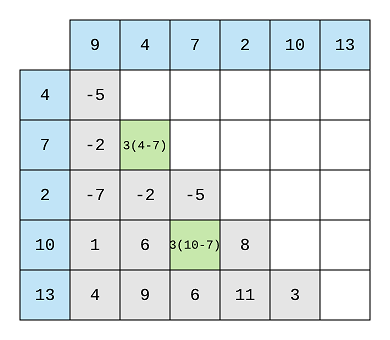
Well, it is there for 10 as 10-7 = 3, so it means that we’ve found first longest arithmetic sequence of length = 3. 4 → 7 → 10.
Apart from 3 there isn’t any other difference that repeats. So, we move to the next column. First we encounter -5. With no presence in the next element, we move to 3. We find that the same difference is present in the 10’s column as well. That is, 13 - 10 is 3 and this will be the 3rd occurrence of 3, 4 → 7 → 10 → 13.
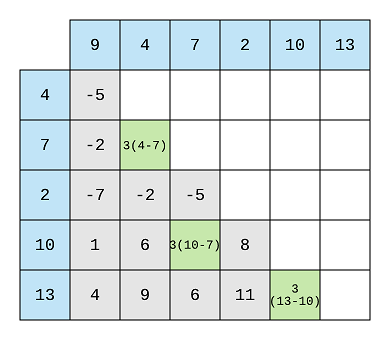
If we move forward with next differences, we won’t find any repeating difference. So, the longest arithmetic subsequence will be 4 → 7 → 10 → 13. This is the brute force approach that I came up with.
What optimization can we do here?
- Here we are finding all the differences first and then checking the repetition of differences.
- If we keep the count of found differences while creating the difference, then we won’t have to repeat the second step of finding the sequences. For example,
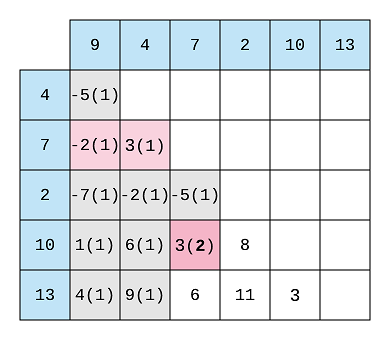
While creating the difference list for 7, we will encounter 3(10 - 7). The moment we get 3 we can check whether any
previous element has the same difference of 3 with 7. The highlighted array, -2, 3 is the list of all the differences
that were made till 7. Here, we find that 3 exists in that array, so we’ll increment the count of found differences to
2(highlighted in bold).
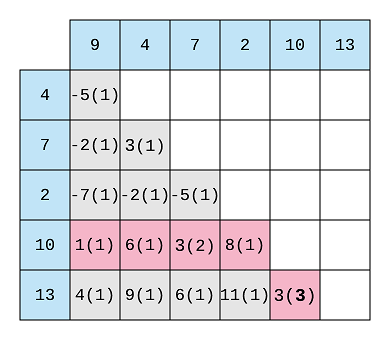
This way when we would find the difference between 13 and 10, we’ll repeat the same method. We will find that3(2) is
present in 10’s array and then we’ll increment the count to 3 for 13.
I hope that you’ve understood the approach now. Let us move to the code for this solution.
You can find the code for the discussed here @ GitHub as well
func longestArithSeqLength(A []int) int {
var cache = make([]map[int]int, len(A))
for i := range cache {
cache[i] = make(map[int]int)
}
maxLength := 0
for i := 0; i < len(A); i++ {
for j := i + 1; j < len(A); j++ {
diff := A[j] - A[i]
cacheMap := cache[i]
increment := false
oldCount, ok := cacheMap[diff]
if ok {
increment = true
}
cacheMap = cache[j]
_, ok = cacheMap[diff]
if !ok {
cacheMap[diff] = 1
}
if increment {
cacheMap[diff] = oldCount + 1
if maxLength < oldCount+1 {
maxLength = oldCount + 1
}
}
}
}
if maxLength == 0 {
return 2
}
// fmt.Println(cache)
return maxLength + 1
}
One small change that you’ll find here is the presence of Maps instead of the array. I used Maps because in our approach we’re looking up the differences if we find one. For example, when we find 3 because of 10-7, we check whether we had found 3 earlier or not while looping for 9 and 4. This check is performed on this Map to get the result in O(1).
I hope that this has helped you to understand the apporach. If this post can be improved then please add a comment below.
