Filling Bookcase Shelves Solution - Leetcode
Understand Leetcode Filling Bookcase Shelves Optimal Solution
This document presents the solution to the problem Filling Bookcase Shelves - Leetcode.
Note: Make sure to go through the code comments as well. It’ll help you understand the concept better.
We have a sequence of books: the i-th book has thickness books[i][0] and height books[i][1].
We want to place these books in order onto bookcase shelves that have total width shelf_width.
We choose some of the books to place on this shelf (such that the sum of their
thickness is <= shelf_width), then build another level of shelf of the bookcase so that the total
height of the bookcase has increased by the maximum height of the books we just put down.
We repeat this process until there are no more books to place.
Note again that at each step of the above process, the order of the books we place is the same
order as the given sequence of books. For example, if we have an ordered list of 5 books, we
might place the first and second book onto the first shelf, the third book on the second shelf,
and the fourth and fifth book on the last shelf.
Return the minimum possible height that the total bookshelf can be after placing shelves in
this manner.
This problem has two arguments, books and width.
The 1st argument, books, is an array of dimensions n x 2, here n is the number of books. books[i][0] is the
width and, books[i][1] is the height of the book at index i.
We’ve to arrange the books in the bookcase, and the bookcase is divided into shelves. The second argument, width is the width of each of the shelves.
This problem requires us to create an arrangement of the books in the shelves such that the height of the bookcase is minimum. One important point to keep in mind is that we’ve to keep the books in the same order in which they are present in the array.

Now, let’s proceed to solve this problem.
We’ll be using this testcase for out approach:
books = {
{1, 1},
{2, 3},
{2, 3}
}
width = 4
Let’s start from the first book. So, How many arrangements can me made with the first book?

A single book can only take one place. This book’s height is 1, so, total height of the bookcase will be 1. It’ll be kept on the first shelf and, the total number of shelves is also 1.
Such arrangements can be represented using:
type arrangement struct {
ShelfNo int
Width int
CurrentShelfHeight int
TotalHeight int
}
Widthcontains total width occupied by the books in the current shelf.CurrentShelfHeightis the height of the current shelf.TotalHeightis the height of the bookcase.- The shelf on which the last arrangement was made is kept in
ShelfNo.
So, the arrangement after adding 1 book to the bookcase is:
arrangement{
ShelfNo: 1,
Width: books[0][0],
CurrentShelfHeight: books[0][1],
TotalHeight: books[0][1],
}
i.e.,
arrangement{
ShelfNo: 1,
Width: 1,
CurrentShelfHeight: 1,
TotalHeight: 1,
}
The second book has the height of 3 units and the width of 2 units. There are two possibilities in which this book can be
arranged:

- It can be kept along with the first book on the same shelf as the width of the shelf is 4, and the width that will be occupied by these two books will be 1 + 2 = 3.
arrangement{
ShelfNo: 1,
Width: 1 + 2,
CurrentShelfHeight: 3,
TotalHeight: 3,
}
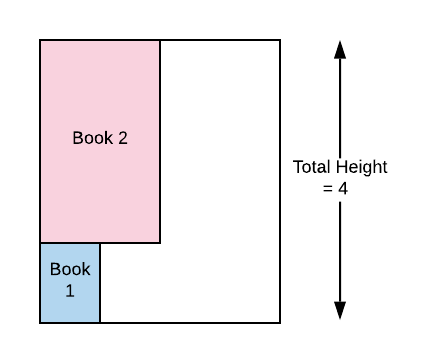
- Or, it can be stored in a new shelf. Please note that this new shelf’s height will be added with the minimum height found in the previous step. In this arrangement the total height of the bookcase will be 1 + 3 = 4, sum of heights of both the shelves.
arrangement{
ShelfNo: 2,
Width: 2,
CurrentShelfHeight: 3,
TotalHeight: 1 + 3,
}
The minimum height of the bookcase will be 3, if we had to store just these two books.
The third book also has the height of 3 units and the with of 2 units. After adding the previous two books, we’re already having two arrangement in which this 3rd book can be added.
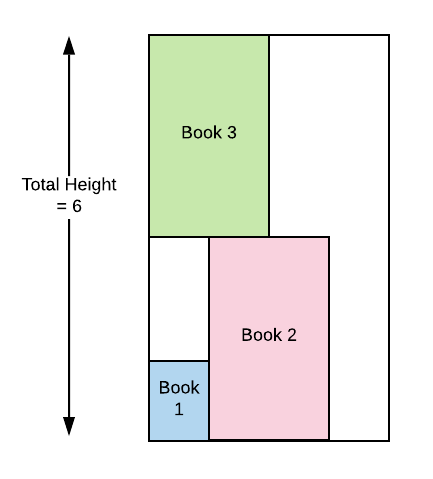
- It cannot be kept along with the 1st and 2nd book because if kep with them the total width becomes 1 + 2 + 2 = 5, and it is greater than 4. So we’ll have to keep it in the next shelf. This way the total height will be 3 + 3 = 6
arrangement{
ShelfNo: 2,
Width: 2,
CurrentShelfHeight: 3,
TotalHeight: 6,
}
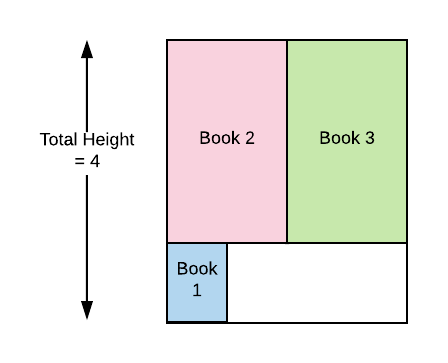
- It can be kept on the 2nd shelf along with the 1st book. This way total height will be 1 + 3 = 4.
arrangement{
ShelfNo: 2,
Width: 4,
CurrentShelfHeight: 3,
TotalHeight: 4,
}

- Or it can be kept on a new shelf. The height of the previous shelf will be equal to the minimum height that we’ve calculated in the previous step, 3.
arrangement{
ShelfNo: 2,
Width: 4,
CurrentShelfHeight: 3,
TotalHeight: 4,
}
So, the minimum total height will be 4, out of 6, 4, 4.
You should also create new test cases as well and follow these steps to find the minimum height of the bookshelf.
Using this process we’re finding the minimum height after adding each of the book. The final solution depends upon the optimal solutions that we’ve found in the previous steps.

Following is the program for the solution, it is based on the these steps:
- Creates a list of arrangement for the current book.
- Find the minimum height from arrangements
- Pick the next book and clear the list of arrangements
type arrangement struct {
ShelfNo int
Width int
CurrentShelfHeight int
TotalHeight int
}
func minHeightShelves(books [][]int, shelf_width int) int {
var shelf []arrangement
var minShelfHeights []int
// create arrangement for the first book
shelf = append(shelf, arrangement{
ShelfNo: 1,
Width: books[0][0],
CurrentShelfHeight: books[0][1],
TotalHeight: books[0][1],
})
minShelfHeights = append(minShelfHeights, books[0][1])
for i := 1; i < len(books); i++ {
currentBook := books[i]
var shelfWithCurrentBook []arrangement
for _, elem := range shelf {
if elem.Width+currentBook[0] <= shelf_width {
// this block is executed if the current book can be
// accommodated in the shelf
newElem := arrangement{
ShelfNo: elem.ShelfNo,
Width: elem.Width + currentBook[0],
CurrentShelfHeight: elem.CurrentShelfHeight,
TotalHeight: elem.TotalHeight,
}
if currentBook[1] > elem.CurrentShelfHeight {
newElem.CurrentShelfHeight = currentBook[1]
newElem.TotalHeight = newElem.TotalHeight + currentBook[1] - elem.CurrentShelfHeight
}
shelfWithCurrentBook = append(shelfWithCurrentBook, newElem)
} else {
// this block is executed if the current book cannot be
// accommodated in the current shelf and a new shelf is created
// for the current book
newElem := arrangement{
ShelfNo: elem.ShelfNo + 1,
Width: currentBook[0],
CurrentShelfHeight: currentBook[1],
TotalHeight: elem.TotalHeight + currentBook[1],
}
shelfWithCurrentBook = append(shelfWithCurrentBook, newElem)
}
}
// a new shelf is also on the minimum height found in the previous
// step
newElem := arrangement{
ShelfNo: shelf[len(shelf)-1].ShelfNo + 1,
Width: currentBook[0],
CurrentShelfHeight: currentBook[1],
TotalHeight: minShelfHeights[i - 1] + currentBook[1],
}
shelfWithCurrentBook = append(shelfWithCurrentBook, newElem)
// here we find the minimum height from all the possible
// arrangements
minShelfHeight := math.MaxInt32
for j := 0; j < len(shelfWithCurrentBook); j++ {
if shelfWithCurrentBook[j].TotalHeight < minShelfHeight {
minShelfHeight = shelfWithCurrentBook[j].TotalHeight
}
}
minShelfHeights = append(minShelfHeights, minShelfHeight)
shelf = shelfWithCurrentBook
}
return minShelfHeights[len(minShelfHeights)-1]
}
