Integer Break Solution - Leetcode
Leetcode Solution: Understand Leetcode problem Integer Break (343) With a Brute Force and Optimal Solution
This document presents the solution to the problem 343. Integer Break. We’ll look into a step by step approach to solve the problem and come up with the optimized way to solve this problem. In the optimized approach, we’ll be breaking the problems into the sub-problems and use an array to store the those solutions. Due to this approach you’ll find the solution for Minimum Cost for Tickets to be similar as well.
Given a positive integer n, break it into the sum of at least two positive integers and maximize
the product of those integers. Return the maximum product you can get.
Example 1:
Input: 2
Output: 1
Explanation: 2 = 1 + 1, 1 × 1 = 1.
Example 2:
Input: 10
Output: 36
Explanation: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36.
Note: You may assume that n is not less than 2 and not larger than 58.
Let’s start with an input that we’ll use for the solving this problem:
input := 10
So, we can reach 10 using the following combinations.
- 5 + 5
- 4 + 6 or 6 + 4
- 3 + 4
- 2 + 8
- 1 + 9
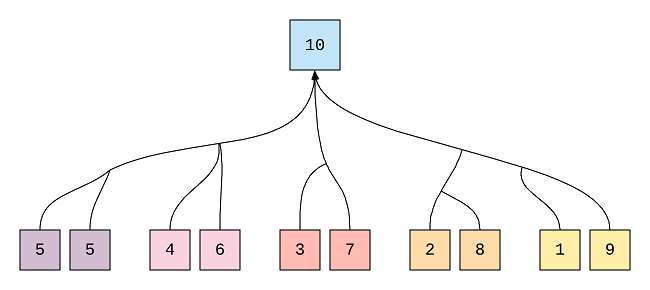
If you’re wondering why I didn’t use combinations containing more than 2 numbers, like 3 + 3 + 2 + 2, it’s because these combinations are already represented by the two number combinations. For example, 5 + 5 represents 3 + 3 + 2 + 2.
This image shows that to know max product for 10 we should already be aware of the max products for 5, 6, 4, 2, 9, 3 and 1 because we can reach 10 using those numbers.
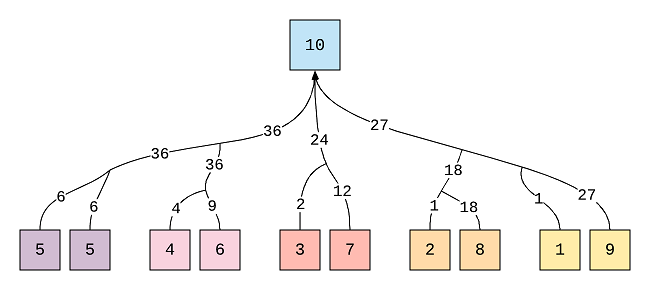
So, to solve for 10 we’ll have to solve it for the numbers that sum up with other numbers to make 10. Once we’ll have the values for the maximum product for each of those numbers then we’ll be able to calculate for 10 as well.
For example, the maximum product for 5 will be 6 because 2 + 3 = 5, 2 x 3 = 6 and it is greater than 1 x 4 = 4. This way, one of the maximum product candidate for 10 will be 6 x 6 = 36 because 5 + 5 = 10. We’ll have to repeat the same process for each of the candidates so that we can find the maximum product by comparing all of them.
So, what do we have to do here?
- We’ve to find the maximum product for each of the numbers so that we can then utilize those maximum products for calculating the maximum products for the larger numbers.
- We’ll be getting multiple candidates for the maximum products, like, for 6 they are 5(1 x 5), 8(2 x 4) and 9(3 x 3). To find the maximum one out of them we’ll have to efficiently store them as well.
Looks like a classic Dynamic Programming approach because
- We’re breaking the problem into sub problem
- We’re using memoization to store the maximum product for each number.
To solve this problem, I’ll be creating an array that will save the maximum product for each number. Let’s call it products.
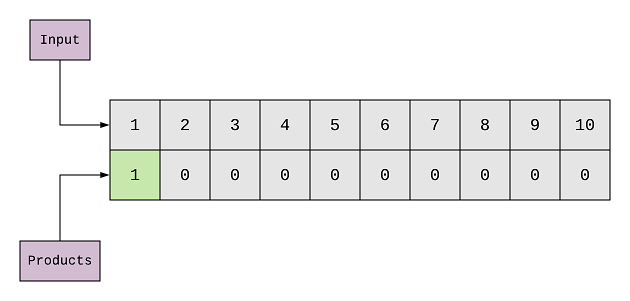
(^)The first element of products is pre-filled with 1.
So, we start with 1, sum it up with all the elements, and we’ll calculate and store the maximum product as well. Then we’ll
repeat the same for 2, 3, 4… until we find the combination where sum > 10.
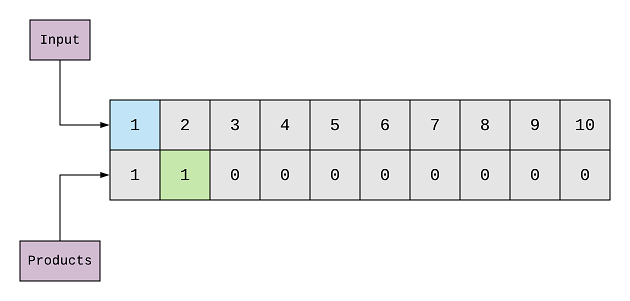
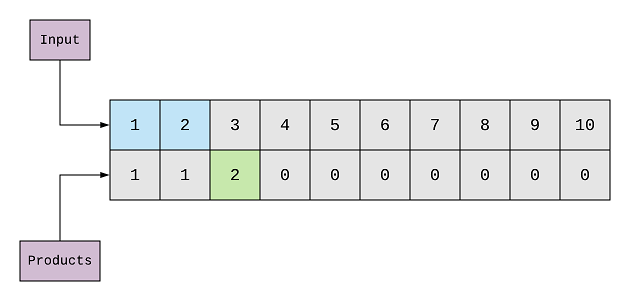
(^)We’ve started here from 1, and the first element is 1 as well. The sum is 2(1 + 1), and the product is 1(1 x 1). So, the
maximum product that we’ve found for 2 is 1. We update the 2nd element of products array with 1.
(^)Then we move to 2, the elements are 1 and 2, and they make the sum = 3(1 + 2) and the product = 2. So, we update the
products array’s 3rd element to 2.
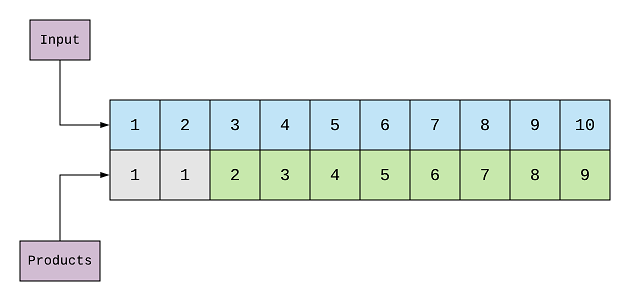
This way we can calculate the sum and the maximum product for each of the elements with 1. Here’s the products array after
one iteration is complete for 1.
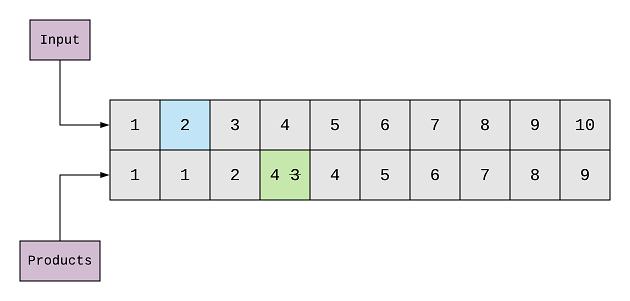
Next we start with 2, and the current element is 2 as well. This way the sum becomes 4 (2 + 2) and product is 4(2 * 2)
as well. Although, we’ve already calculated the product for 4 in the previous step(1, 3) but the current product is greater
than the previous product, ie, 3 < 4, so, we update the 4th element of the products array to 4.
Same, with 2 and 3, the sum is 5, and the product is 6, so we update the 5th element of the products array to 6 as it is greater than the previous product(6 > 4).
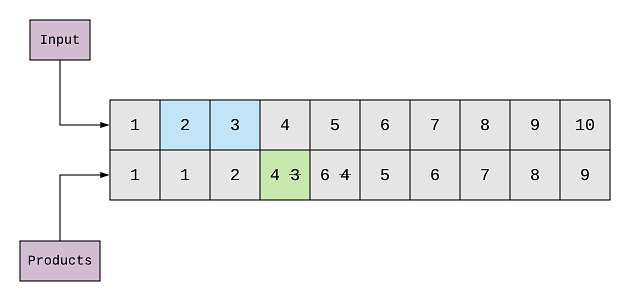
This way we can calculate the sum and the maximum product for each of the elements with 2. Here’s the products array after
one iteration is complete for 2.
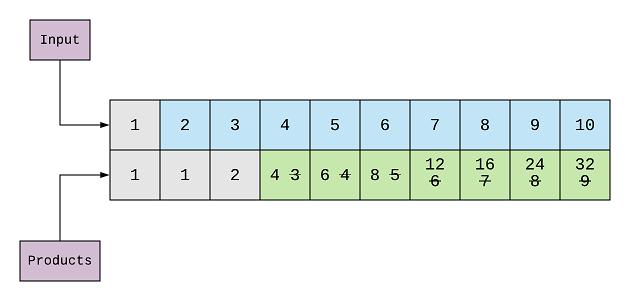
Using the same approach, we can calculate the maximum products for all the elements with 3. The highlighted items in green color are those elements whose values got updated.
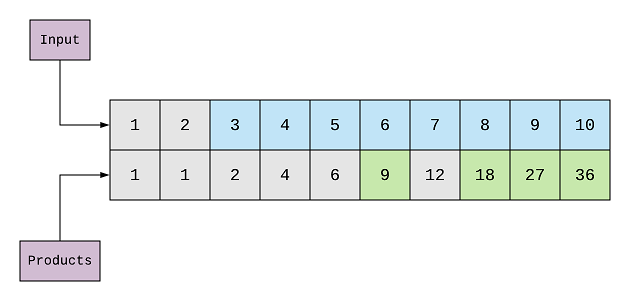
This way if you would do it for all the elements(until you find the sum of the two elements < 10), the products array
will convert into:
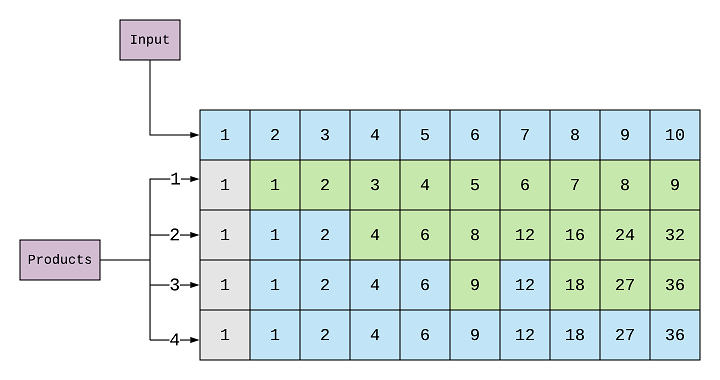
This(^) show the stage of the array after 4 iterations are complete. I’ve not added product array’s image after 4 iterations because it doesn’t change after that. Again, the highlighted elements in green display a change in the value.
The last value of the product’s array contains the answer, 36. I hope you were able to understand the approach. Please do let me know in the comments below if you’ve any doubt, or a better way to solve this. Let’s look into the code now. It is available here @ GitHub as well.
func integerBreak(n int) int {
// the products array is created here.
// the size is constant because Leetcode says that they won't provide a number > 59
var products = make([]int, 59)
// setting the first element to 1
products[1] = 1
for i := 1; i <= n; i++ {
for j := i; j <= n; j++ {
sum := i + j
if sum <= n {
productI := products[i]
if productI < i {
// for 2, the product is 1 because of 1 x 1
// however it is lower than 2
// so we'll be using the 2 as product instead
productI = i
}
productJ := products[j]
if productJ < j {
productJ = j
}
oldProduct := products[sum]
if oldProduct < productI*productJ {
products[sum] = productI * productJ
}
} else {
break
}
}
fmt.Println(products)
}
return products[n]
}
(^)Here is the code for the solution that we’ve discussed. The products array in the code is the same array that we’ve
been discussing throughout the article.
