Longest Zig Zag Path in a Binary Tree Solution - Leetcode

Leetcode Solution: Understand Leetcode problem Longest Zig Zag Path in a Binary Tree With a Brute Force and Optimal Solution

01 August 2020

This document presents the solution to the problem 1372. Longest ZigZag Path in a Binary Tree - Leetcode. We’ll look into the step by step approach to solve the problem and come up with the optimized way to solve this problem.

		
				
Given a binary tree root, a ZigZag path for a binary tree is defined as follow:
                                                           
Choose any node in the binary tree and a direction (right or left).
If the current direction is right then move to the right child of the current node otherwise move to the left child.
Change the direction from right to left or right to left.
Repeat the second and third step until you can't move in the tree.
                                                           
Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).

Return the longest ZigZag path contained in that tree.

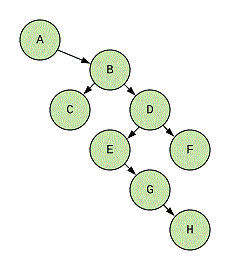
Let’s start with an example that we’ll use for the solving this question:

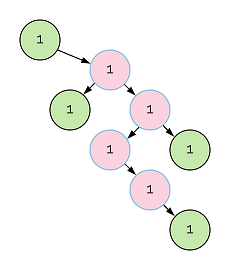
We’ll use this example, however, there’s a change that I’ll do here. The tree nodes have this struct:

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

But the problem solving does not require the data of node, so I’ll remove it and add an identifier for each of the node for reference.

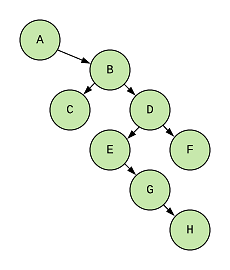
Here we see that B → D → E → G is the longest zig zag path with length = 3. Along with that there are two other zig zag paths with length = 2, they are A → B → C and D → E → G.

Let’s start traversing this tree from the root, A. As B is the only right child of A so this will be counted in the zig zag path A → B, and the length will be 1.

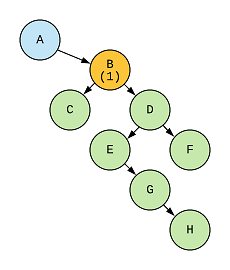
Now we’re at B, from here we can go to C or D. If we go to C then the zig zag path will remain valid and C will be added the previous path, A → B → C. The path length at C is 2.

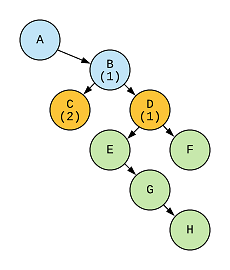
But the path length at D is 1 because as D is the right child of, and the zig zag path breaks here. The value 1 means here that the path is B → D and not A → B → D because a new path started from B.

So, we have increased the path length whenever we move to left(right) child of a node that is the right(left) child of its parent, like, C is the left child of B and B is the right child of A and the zig zag continues.
We update the path value to 1 whenever we traverse to the right(left) child of a node that is also a right(left) child of its parent, like, D is the right child of B and B is the right child of A.

As C does not have any children, so we’ll have to move to D. From D the zig zag path continues to E making the length of the path as 2 while the path breaks when we reach to F from D.

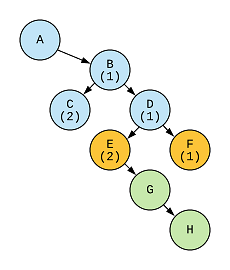
Then we reach to G from E, and the zig zag path present at E continues making the length = 3 at G.

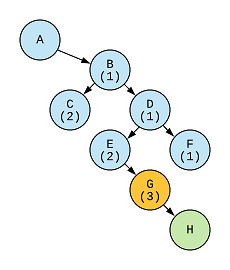
Here is the entire tree traversal while finding the length of the largest path:

The tree traversal that we’ll follow here will look somewhat similar to a pre order traversal. What we’ll do here is:

We’ll traverse through each of the nodes while passing the length accumulated till that node as well.
We will increase the count if the zig zag continues
We’ll reset the count to 1 whenever there’s a break in the zig zag path.

Here is the function that will do the pre order traversal for us:

// this function traverses through all the nodes.
// the parameter left is true if the current node is the left
// child of it's parent otherwise its false
func traverse(node *TreeNode, length int, left bool, maxLength *int) {
	if length > *maxLength {
		*maxLength = length
	}
	if node.Left != nil {
		if left {
			traverse(node.Left, 1, true, maxLength)
		} else {
			traverse(node.Left, length+1, true, maxLength)
		}
	}
	if node.Right != nil {
		if left {
			traverse(node.Right, length+1, false, maxLength)
		} else {
			traverse(node.Right, 1, false, maxLength)
		}
	}
}

Here you’d notice that we’re incrementing the length for the left child if the current node is a right child and vice versa. Also, we keep the maximum length counted till now in the variable maxLength.

And, here is the actual function that calls the traverse function, it is also available here @ GitHub:

func longestZigZag(root *TreeNode) int {
	if root == nil {
		return 0
	}
	if root.Left == nil && root.Right == nil {
		return 0
	}
	leftLength := 0
	rightLength := 0
	if root.Left != nil {
		traverse(root.Left, 1, true, &leftLength)
	}
	if root.Right != nil {
		traverse(root.Right, 1, false, &rightLength)
	}
	if leftLength > rightLength {
		return leftLength
	}
	return rightLength
}

Loading Comments... Disqus Loader

Longest Zig Zag Path in a Binary Tree Solution - Leetcode

Leetcode Solution: Understand Leetcode problem Longest Zig Zag Path in a Binary Tree With a Brute Force and Optimal Solution

Related Pages: