Construct Binary Search Tree From Preorder Traversal Solution
Leetcode Solution: Understand Leetcode problem Construct Binary Search Tree From Preorder Traversal(1008) Solution
In this article we’ll be solving the problem: Construct Binary Search Tree from Preorder Traversal. Just like the problem, Maximum Binary Tree and Convert Sorted Array to BST, this problem falls into the category of those problems in which the tree is created from an input array.
Return the root node of a binary search tree that matches the given preorder traversal.
(Recall that a binary search tree is a binary tree where for every node, any descendant
of node.left has a value < node.val, and any descendant of node.right has a value > node.val.
Also, recall that a preorder traversal displays the value of the node first, then traverses
node.left, then traverses node.right.)
It's guaranteed that for the given test cases there is always possible to find a binary search
tree with the given requirements.
Example 1:
Input: [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]
8
/ \
5 10
/ \ \
1 7 12
Constraints:
1 <= preorder.length <= 100
1 <= preorder[i] <= 10^8
The values of preorder are distinct.
The array will contain the pre order tree traversal for the binary search tree. Since it’s a pre order tree traversal output it means that the first element from the array will be the root element and since it’s a binary search tree the elements in the left subtree will be those elements that are lower than the first element(root), and the elements greater than the first element will form the right subtree.
We’ll be using the following array as the example input to understand the solution:
input := []int{8, 5, 1, 7, 10, 12}
To solve this problem, we’ll
- pick the first element and make it the root (
8) - find the elements for the left subtree (
5, 1, 7) - find the elements for the right subtree (
10, 12) - perform the steps 1, 2, 3 on the array found in step 2
- perform the steps 1, 2, 3 on the array found in step 3
Here’s the first split that we’ve done after finding 8 as the root element:
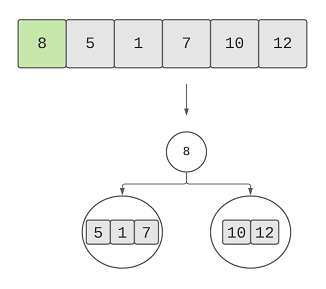
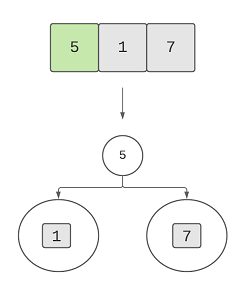
We found two sub arrays that’ll be two subtrees. In the left subtree, we find 5 as the root of the left subtree and then
we divide the array into two parts, [1] and [7] as 5 was the first element in that sub array.
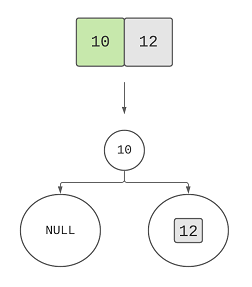
We’ve completed the left sub tree. Now, we’re moving to the right subtree, [10, 12]:
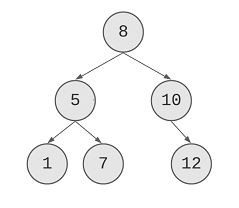
Finally, here’s the tree that we’ve created through from the previous steps:
Here is the program for that:
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func bstFromPreorder(preorder []int) *TreeNode {
if len(preorder) == 0 {
return nil
}
return construct(preorder, 0, len(preorder) - 1)
}
func construct(preorder []int, start, end int) *TreeNode {
if start > len(preorder) || start < 0 || end > len(preorder) || start > end {
return nil
}
val := preorder[start]
partition := findPartition(preorder, val, start, end)
node := &TreeNode {
Val: val,
}
if partition == -1 {
node.Left = construct(preorder, start + 1, end)
} else {
node.Left = construct(preorder, start + 1, partition - 1)
}
node.Right = construct(preorder, partition, end)
return node
}
func findPartition(preorder []int, val, start, end int) int {
fmt.Println(val, start, end)
if start > len(preorder) || start < 0 || end > len(preorder) || start > end {
return -1
}
for i := start; i <= end; i++ {
if preorder[i] > val {
return i
}
}
return -1
}
The logic remains same to what we’ve discussed earlier. The function bstFromPreorder calls the function
construct by passing the entire array. Then construct calls itself recursively after finding the partition index
and dividing the array into sub array. Here, we’re not actually dividing the array as we’re finding the start and the
end indices on which function has to operate as the sub problem. The function findPartition is a very simple
function with the responsibility of finding the partition index from the array between the start and the end indices.
This program can be found on GitHub as well.
