Maximum Depth of N Ary Tree - Leetcode

Leetcode Solution: Understand and solve Leetcode problem Maximum Depth of N Ary Tree(559)

25 August 2020

In this article we’ll be solving the problem: Maximum Depth of N-ary Tree. This problem belongs to Tree Traversal category and just like the problem, Increasing Order Search Tree, and Merge Two Binary Trees this problem also requires a slight modification in a simple Tree Traversal approach.

		
				
Given a n-ary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the 
farthest leaf node.

Nary-Tree input serialization is represented in their level order traversal, each group of 
children is separated by the null value (See examples).

Constraints:
    The depth of the n-ary tree is less than or equal to 1000.
    The total number of nodes is between [0, 10^4].

As mentioned earlier, this problem requires a small change in the tree traversal function. To solve this problem, I’ll be using the preOrder tree traversal. Here’s the tree that’ll be our example:

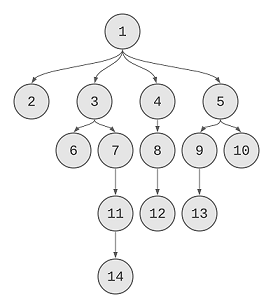
While traversing the tree using the pre order approach, we’ll also pass an integer to each of the node. This integer will be the current depth. Once we reach to a node, we’ll increment the depth by 1 and then pass the depth to all of its children.

There will also be one more variable, maxDepthValue, that’ll contain the maximum value for the depth that a node has ever received and while traversing the nodes we’ll update the maxDepthValue's.

Here the code for that:

type Node struct {
	Val      int
	Children []*Node
}

// maxDepthValue contains the maximum depth a node has ever received.
// While traversal, the current height is compared with this variable.
// If the current height is greater than maxDepth then maxDepthValue is updated
// with the current height
var maxDepthValue int

func maxDepth(root *Node) int {
	maxDepthValue = 0
	if root == nil {
		return 0
	}
	preOrder(root, 0)
	return maxDepthValue
}

func preOrder(root *Node, currentDepth int) int {
	currentDepth++
	if currentDepth > maxDepthValue {
		maxDepthValue = currentDepth
	}
	if root.Children != nil {
		for _, child := range root.Children {
			preOrder(child, currentDepth)
		}
	}
	return 0
}

This code is available here @ GitHub as well.

Here, preOrder is called by maxDepth function and then preOrder calls itself recursively for each of the children.

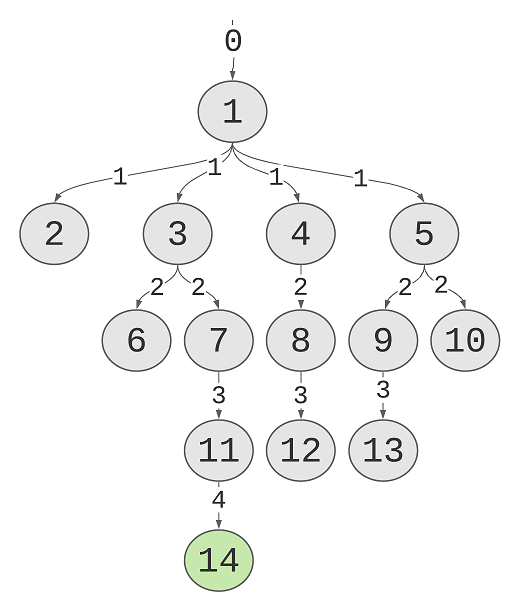
This image presents the values for currentDepth after every execution of preOrder

Loading Comments... Disqus Loader

Maximum Depth of N Ary Tree - Leetcode

Leetcode Solution: Understand and solve Leetcode problem Maximum Depth of N Ary Tree(559)

Related Pages: