Diameter of Binary Tree Solution

Leetcode Solution: Understand and solve Leetcode problem Diameter of Binary Tree(543)

13 September 2020

In this article we’ll be solving the problem: Diameter of Binary Tree. Just like the problem, Convert BST to Greater Tree and Merge Two Binary Trees, this problem also requires a some modification in a simple Tree Traversal approach.

		
				
Given a binary tree, you need to compute the length of the diameter of the tree.
The diameter of a binary tree is the length of the longest path between any two
nodes in a tree. This path may or may not pass through the root.

Example:
    
    Given a binary tree

          1
         / \
        2   3
       / \     
      4   5    

    Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].

Note: The length of path between two nodes is represented by the number of edges between them.

We’ll be using the following tree as an example input:

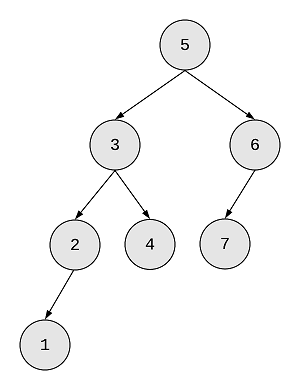
To solve this problem, we’ve to find the longest diameter of the tree and for that we’ve to find the length of the path between any two nodes of the tree. Also, this path may or may not pass through the root.

The longest path for the example tree is:

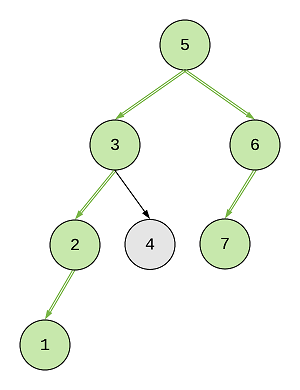
However, while we’re in the process of finding the diameter of the tree, we’ll find a lot of them, like, this one:

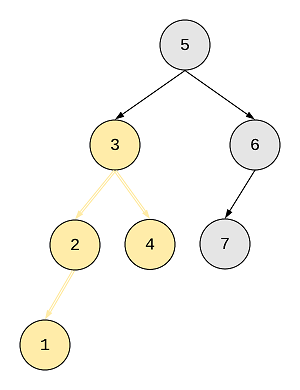
Here the length of the diameter will be 3 (1 -> 2 -> 3 -> 4) but this is not the actual diameter of the tree. However, the left path of this diameter is part of the longest diameter, so, we’ll pass the longest of the right or the left path back to the parent node.

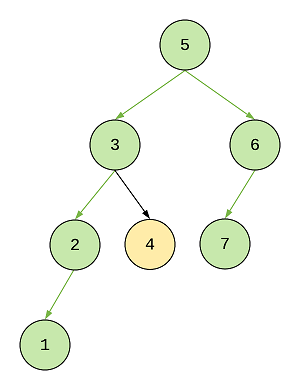
Here is the program for that:

type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}

var maxDiameter int
func diameterOfBinaryTree(root *TreeNode) int {
	maxDiameter = 0
	postOrder(root)
	return maxDiameter
}

func postOrder(node *TreeNode) int {
	if node == nil {
		return 0
	}
	leftSize := postOrder(node.Left)
	rightSize := postOrder(node.Right)
    
    // calculating the current diameter
	currentDiameter := leftSize + rightSize
	if currentDiameter > maxDiameter {
        // updating the maximum diameter if the current diameter
        // if the current diameter is greater
		maxDiameter = currentDiameter
	}
    // then longest of the left or the right path is return 
	if leftSize > rightSize {
		return leftSize + 1
	}
	return rightSize + 1
}

This program is available on GitHub as well. Here we’re using the Post Order tree traversal approach.

Loading Comments... Disqus Loader

Diameter of Binary Tree Solution

Leetcode Solution: Understand and solve Leetcode problem Diameter of Binary Tree(543)

Related Pages: