Convert BST to Greater Tree Solution - Leetcode

Leetcode Solution: Understand and solve Leetcode problem Convert BST to Greater Tree Solution(538)

05 September 2020

In this article, we’ll be solving the problem: Convert BST to Greater Tree. Just like the problems, Univalued Binary Tree and Leaf Similar Trees this problem belongs to Tree Traversal and Recursion category.

		
				
Given a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original
BST is changed to the original key plus sum of all keys greater than the original key in BST.

Example:
    Input: The root of a Binary Search Tree like this:
                  5
                /   \
               2     13
    
    Output: The root of a Greater Tree like this:
                 18
                /   \
              20     13

The provided tree will always be a Binary Search Tree(BST). This means that if we traverse the elements from right to left we’ll be traversing it in a decreasing order. For example, if the tree is:

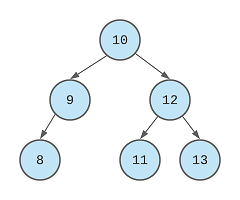
then we’ll get 13, 12, 11, 10, 9, 8 (in that order) if we traverse from right to left. This order is decreasing order. We’ll use this tree traversal approach to solve this problem. We’ll first visit the right child of a node, then the node itself and then the left child of the node. This way, we’ll go to 13 then to 12 then to 11 and so on.

Along with traversing the nodes, we’ll update the node value by adding the value of the previous node as well. For example, we’ll go to 13, then to 12, here we’ll update the value to 25(12 + 13) and pass this value to 11. At 11, we’ll update the value to 36(11 + 25) traverse to 10.

This image shows the updated tree once the traversal is complete.

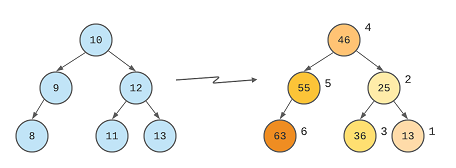
This way we’ve converted the tree to a Greater Tree. Here is the program for it:


type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func convertBST(root *TreeNode) *TreeNode {
	rightOrder(root, 0)
	return root
}

func rightOrder(node *TreeNode, valueToAdd int) int {
	if node == nil {
		return 0
	}
	if node.Right != nil {
		valueToAdd = rightOrder(node.Right, valueToAdd)
	}
	node.Val += valueToAdd
	valueToAdd = node.Val
	if node.Left != nil {
		return rightOrder(node.Left, valueToAdd)
	}
	return valueToAdd
}

This is available @ GitHub as well.

Loading Comments... Disqus Loader

Convert BST to Greater Tree Solution - Leetcode

Leetcode Solution: Understand and solve Leetcode problem Convert BST to Greater Tree Solution(538)

Related Pages: