Cousins in Binary Tree Solution
Leetcode Solution: Understand Leetcode problem Cousins in Binary Tree(993) Solution
In this article we’ll be solving the problem: Cousins in Binary Tree. Just like the problem, Same Tree or Equal Tree and Leaf Similar Trees, this problem also requires a Tree Traversal approach to find the nodes in the tree.
In a binary tree, the root node is at depth 0, and children of each depth k node are at depth
k+1.
Two nodes of a binary tree are cousins if they have the same depth, but have different parents.
We are given the root of a binary tree with unique values, and the values x and y of two
different nodes in the tree.
Return true if and only if the nodes corresponding to the values x and y are cousins.
Example 1:
Input: root = [1,2,3,4], x = 4, y = 3
1
/ \
2 3
/
4
Output: false
Example 2:
Input: root = [1,2,3,null,4,null,5], x = 5, y = 4
1
/ \
2 3
\ \
4 5
Output: true
Example 3:
Input: root = [1,2,3,null,4], x = 2, y = 3
1
/ \
2 3
\
4
Output: false
Constraints:
The number of nodes in the tree will be between 2 and 100.
Each node has a unique integer value from 1 to 100.
The solution to this problem is not difficult. It is based on the Tree Traversal, depth of the current node and the parent of the current node being traversed. To keep track of the depth of the current node, we can pass an integer from the parent node to the children node after incrementing it. This way the variable will always contain the depth of current node.
Along with passing the depth value, a parent will also pass it’s own pointer as well to the children nodes so the children nodes can access their parent.
Once we reach the node that we’ve to find, we’ll return the depth and the parent of the node. Then we’ll repeat this approach for the other node. This way we’ll have both nodes’ parents and depth. If these two nodes are cousins then they will have the same height but different parent.
Here’s an image showing the traversal of an example tree. Here, we’re searching if 4 exists in the tree:
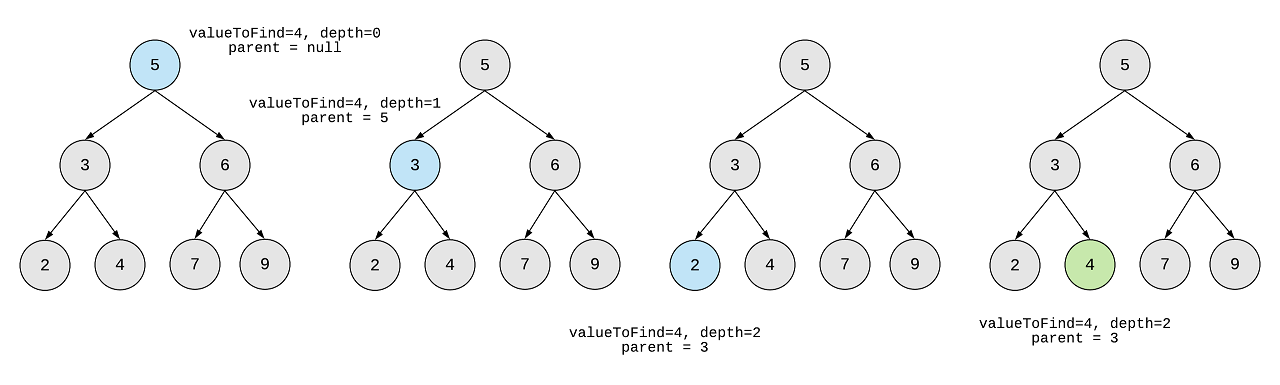
Then we’re searching for 7 in this image:
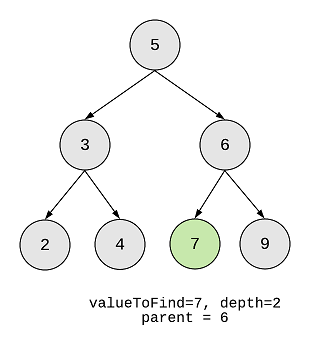
Since, 4 and 7 have same height but different parent they are cousins.
Here’s the code for this problem. It can be found here on GitHub as well.
func isCousins(root *TreeNode, x int, y int) bool {
parent1, height1 := preOrder(root, nil, x, 0)
parent2, height2 := preOrder(root, nil, y, 0)
if height1 == height2 && height1 != -1{
return parent1 != parent2
}
return false
}
func preOrder(node, parent *TreeNode, val, height int) (*TreeNode, int) {
if node.Val == val {
return parent, height
}
if node.Left != nil {
foundParent, foundHeight := preOrder(node.Left, node, val, height + 1)
if foundParent != nil && foundHeight != -1 {
return foundParent, foundHeight
}
}
if node.Right != nil {
foundParent, foundHeight := preOrder(node.Right, node, val, height + 1)
if foundParent != nil && foundHeight != -1 {
return foundParent, foundHeight
}
}
return nil, -1
}
Here the function isCousins calls preOrder to traverse the tree. The preOrder function is check if the node with
value,val, exists and then returns its parent and the height. isCousins then checks if the provided nodes are cousins
by comparing their heights and parents.
