Merge Two Binary Trees Solution
Leetcode Solution: Understand and solve Leetcode problem Merge two binary trees(617)
In this article we’ll be solving the problem: Merge Two Binary Trees. Just like the problem, Range Sum of BST, this problem also requires a slight modification in a simple Tree Traversal approach.
Given two binary trees and imagine that when you put one of them to cover the other, some nodes of
the two trees are overlapped while the others are not.
You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then
sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used
as the node of new tree.
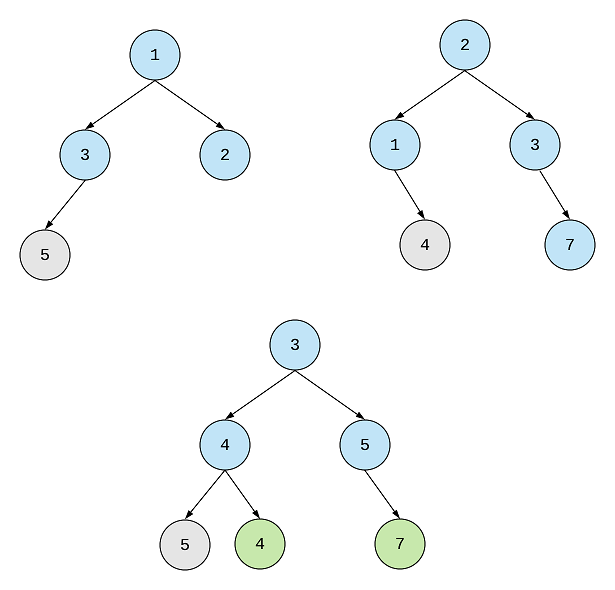
Example 1:
Input:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
Output:
Merged tree:
3
/ \
4 5
/ \ \
5 4 7
We’ll be using the following tree as the input to solve the problem:
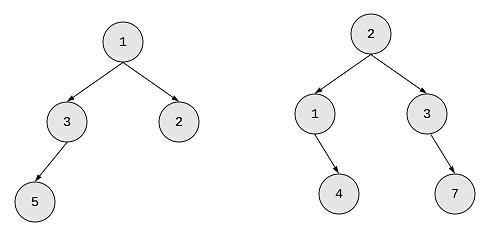
As mentioned earlier, the solution to this question require some change in the tree traversal. Since, we’ve to merge these two trees, we may find following cases:
- There are two nodes for the same position. For example, both the trees have root nodes, so, the resulting tree’s root node’s value will be the sum of the values of the root nodes of both the trees.
- Both the nodes will not have the left children. For example, the node with value 3 in left tree has a left child, but the node with value 1 in the right tree doesn’t have a left child. In this case the resulting tree’s node will get the left child from the left tree.
- Both the nodes will not have the right children. For example, the node with value 1 in right tree has a right child, but the node with value 3 in the left tree doesn’t have a right child. In this case the resulting tree’s node will get the right child from the right tree.
- In the steps, 2 and 3, we ‘re just copying the child from one of the parent as both the parent do not have it. It means that we do not have to traverse those new nodes to sum the values like we did in the 1st step.
Let’s start with the example then:
-
We’ll simply traverse both the tress simultaneously using the
inOrderapproach. I’ve created the resulting tree as a duplicate of the first tree. The very first node will be the root nodes. The resulting tree’s root node will be sum of both the values.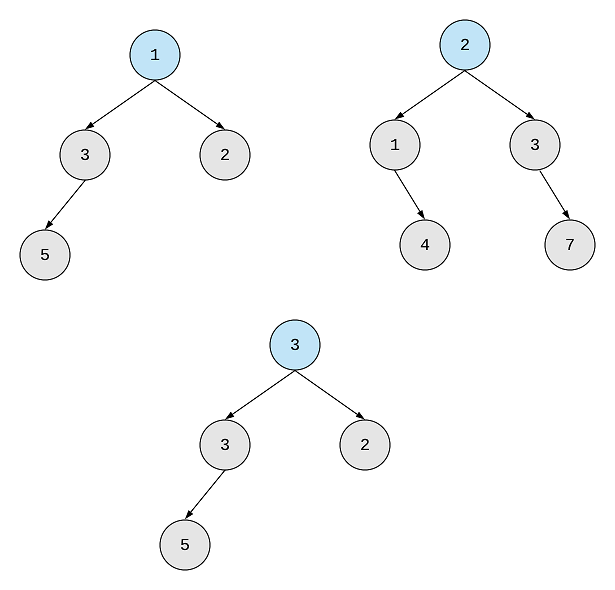
-
Next, we get 3 and 1, so the merged tree will have 4 at that place.
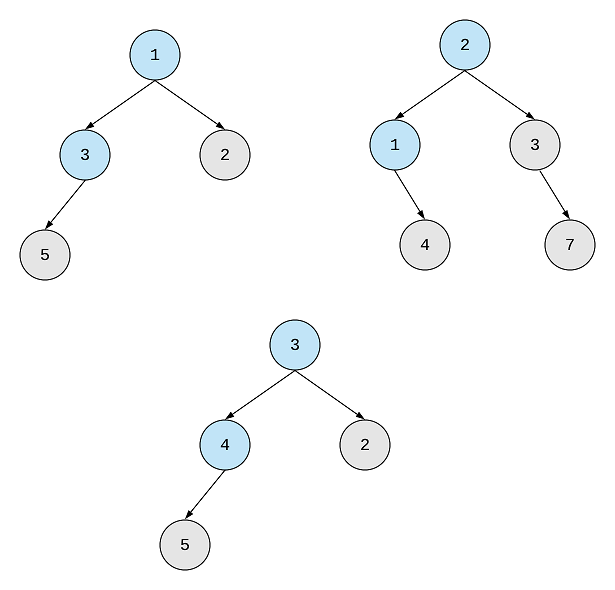
-
Left tree’s 3 has 5 as the left child, but the right tree’s 1 doesn’t have a left child. So the merge tree will remain same. However, right tree’s 1 has a right child while left tree’s 3 does not have a right child. So, we copy that into the resulting tree.
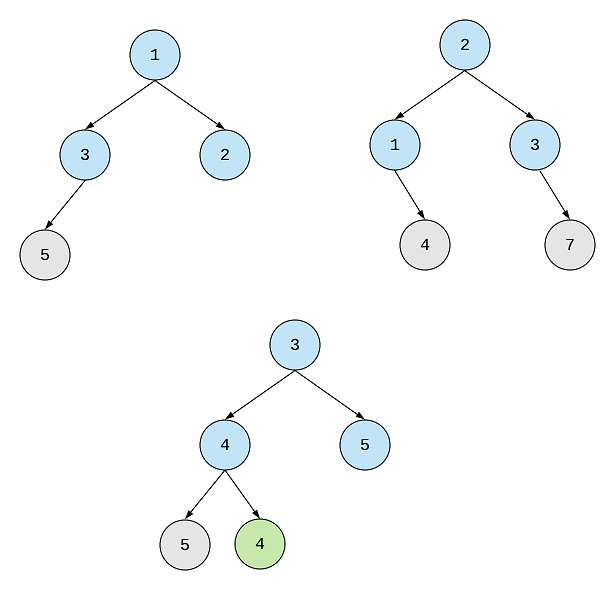
-
This way we update the root’s right node, and the right node of the root’s right node as well.
Here’s the code for this problem. It can be found here on GitHub as well.
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func mergeTrees(t1 *TreeNode, t2 *TreeNode) *TreeNode {
// validation
if t1 == nil && t2 == nil {
return nil
}
// validation
if t1 == nil && t2 != nil {
return t2
}
// validation
if t1 != nil && t2 == nil {
return t1
}
// sum if both the nodes have values
if t1 != nil && t2 != nil {
t1.Val += t2.Val
}
// proceed to inOrder if both the nodes have left child
if t1.Left != nil && t2.Left != nil {
mergeTrees(t1.Left, t2.Left)
}
// proceed to inOrder if both the nodes have right child
if t1.Right != nil && t2.Right != nil {
mergeTrees(t1.Right, t2.Right)
}
// copy the left node from the right tree if the left doesn't have one
if t1.Left == nil && t2.Left != nil {
t1.Left = t2.Left
}
// copy the right node from the right tree if the left doesn't have one
if t1.Right == nil && t2.Right != nil {
t1.Right = t2.Right
}
return t1
}
Here the function mergeTrees is the modified inOrder tree traversal. It sums up the values if both the nodes are not
null, otherwise, it copies the missing child from the right tree.
