Maximum Binary Tree Solution
Leetcode Solution: Understand Leetcode problem Maximum Binary Tree(654) Solution
In this article we’ll be solving the problem: Maximum Binary Tree. Just like the problem, Convert Sorted Array to BST and Deepest Leaves Sum, this problem also requires the creation of a binary tree from an array in which the element selection for the root position depends on a criterion.
Given an integer array with no duplicates. A maximum tree building on this array is defined as
follow:
The root is the maximum number in the array.
The left subtree is the maximum tree constructed from left part subarray divided by the
maximum number.
The right subtree is the maximum tree constructed from right part subarray divided by
the maximum number.
Construct the maximum tree by the given array and output the root node of this tree.
Example 1:
Input: [3,2,1,6,0,5]
Output: return the tree root node representing the following tree:
6
/ \
3 5
\ /
2 0
\
1
Note:
The size of the given array will be in the range [1,1000].
The problem is actually pretty easy to understand but the solution might get a little tricky because of the recursions for creating the nodes of the tree.
To solve this problem, we’ve to find the maximum element and its index in the array and then create a node with the
same maximum element value. This operation will create two sub arrays, one on the left side of the index and one on the
right side. Then, we’ve to perform the same operation on the sub arrays to create the left, and the right sub trees for
that node.
We’ll be using the following array as the example input to understand the solution:
input := []int{3, 2, 1, 6, 0, 5}
Here’s the first split that we’ve done after finding 6 as the maximum element:
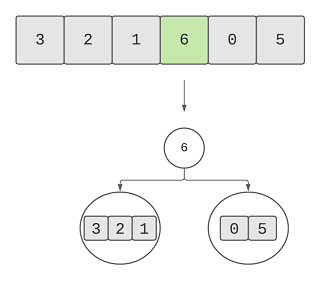
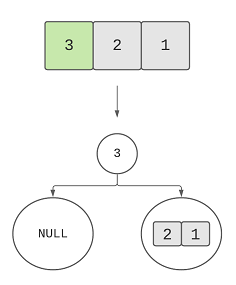
We found two sub arrays that’ll be two subtrees. In the left subtree, we find 3 as the root of the left sub tree and then
we divide the array into two parts, null and [1, 2] as 3 was the first element in that sub array.
Same way, we can work on the sub array [2, 1] created after the previous step:
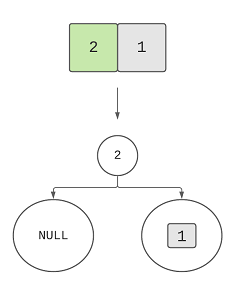
We’ve completed the left sub tree. Now, we’re moving to the right subtree, [0, 5]:
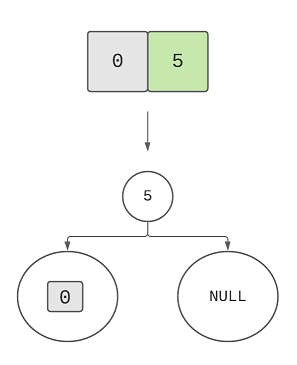
Finally, here’s the tree that we’ve created through from the previous steps:
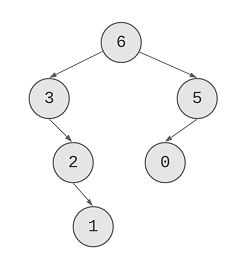
Here is the program for that:
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func constructMaximumBinaryTree(nums []int) *TreeNode {
if len(nums) == 0 {
return nil
}
return createNode(nums, 0, len(nums) - 1)
}
func createNode(nums []int, start, end int) *TreeNode {
if start > end {
return nil
}
max, index := findMax(nums, start, end)
if max == -1 || index == -1 {
return nil
}
return &TreeNode {
Val: max,
Left: createNode(nums, start, index - 1),
Right: createNode(nums, index + 1, end),
}
}
func findMax(nums []int, start, end int) (int, int) {
if start < 0 || end > len(nums) - 1 || start > end {
return -1, -1
}
max := -1
index := -1
for i := start; i <= end; i++ {
if nums[i] > max {
max = nums[i]
index = i
}
}
return max, index
}
The logic remains same to what we’ve discussed earlier. The function constructMaximumBinaryTree calls the function
createNode by passing the entire array. Then createNode calls itself recursively after finding the maximum element
and dividing the array into sub array. Here, we’re not actually dividing the array as we’re finding the start and the
end indices on which function has to operate as the sub problem. The function findMax is a very simple function with
the responsibility of finding the maximum element from the array between the start and the end indices.
This program can be found on GitHub as well.
