Convert Sorted Array to Binary Search Tree Solution

Leetcode Solution: Understand and solve Leetcode problem Convert Sorted Array to Binary Search Tree(108)

05 September 2020

In this article, we’ll be solving the problem: Convert Sorted Array to Binary Search Tree. Just like the problems, Leaf Similar Trees and Sum of Root to Leaf Binary Numbers this problem belongs to Tree Traversal and Recursion category.

		
				
Given an array where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of
the two subtrees of every node never differ by more than 1.

Example:
    Given the sorted array: [-10,-3,0,5,9],
    
    One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:
    
          0
         / \
       -3   9
       /   /
     -10  5

The input array will always be a sorted array because we’ve to create a Binary Search Tree(BST) out of it. Given a sorted array, there can be multiple sorted BSTs. For example, the array, [-10,-3,0,5], can be converted into multiple BSTs. Some of them are:

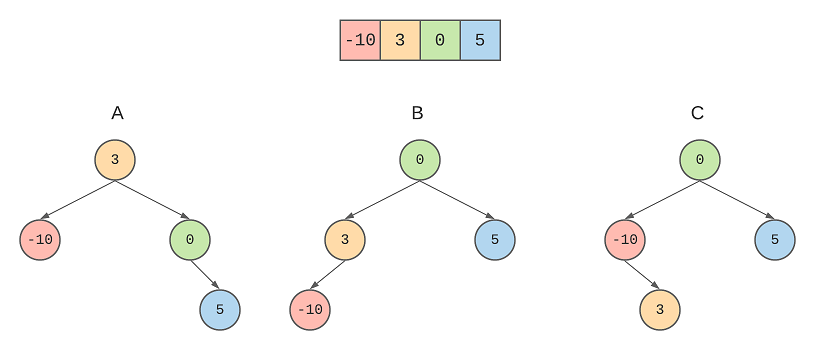
The solution also requires us create a BST that must be height balanced as well, i.e., the depth of the left and right sub tree must not differ by more than 1. All the trees in the previous image are height balanced.

So, to keep the BST height balanced, we’ll be picking the root from the middle of the array. This root element will divide the array into two parts, left and right. All the elements in the left half will become the elements of the left subtree and all the elements of the right half will become the elements of the right subtree. Then we’ll have to apply the same process on the left half, and the right half as well. A perfect recursion example(or Divide and Conquer?)!

This image provides the approach to solve this problem:

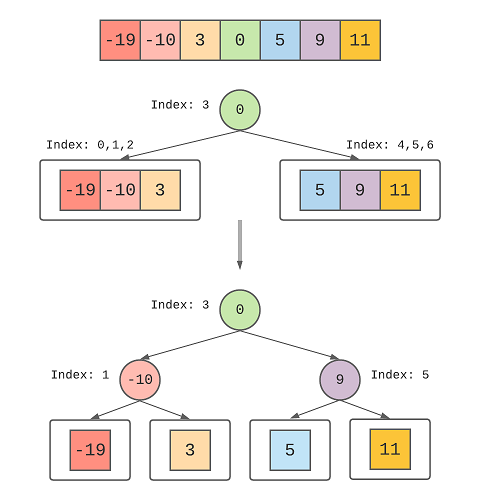
Here, we’ve picked the element at the 3rd index as the root because it’s in the middle and then the elements from index 0, 2 become the part of left subtree, and the elements from index 4, 6 become the part of the right subtree.

Then we repeat the same process on the array elements from index 0, 2 and 4, 6. Out of that we select the element at the index 1 and 5 as the root element for the left, and the right subtree respectively.

This process will be repeated until the start index is lesser than the end index just like how to stop the search in a Binary search tree.

Here is the code for the solution that we discussed:

// Definition for a binary tree node.
type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func sortedArrayToBST(nums []int) *TreeNode {
	return findRootAndDivide(nums, 0, len(nums) - 1)
}

func findRootAndDivide(nums []int, startIndex, endIndex int) *TreeNode {
	if startIndex > endIndex {
		return nil
	}
	midIndex := (startIndex + endIndex) / 2
	return &TreeNode{
		Val:   nums[midIndex],
		Left:  findRootAndDivide(nums, startIndex, midIndex-1),
		Right: findRootAndDivide(nums, midIndex+1, endIndex),
	}
}

This is available @ GitHub as well.

Loading Comments... Disqus Loader

Convert Sorted Array to Binary Search Tree Solution

Leetcode Solution: Understand and solve Leetcode problem Convert Sorted Array to Binary Search Tree(108)

Related Pages: