Two Sum IV - Input is a BST Solution - Leetcode

Leetcode Solution: Understand and solve Leetcode problem Two Sum IV - Input is a BST Solution(653)

06 September 2020

In this article, we’ll be solving the problem: Two Sum IV - Input is a BST. Just like the problems, Univalued Binary Tree and Leaf Similar Trees this problem belongs to Tree Traversal and Recursion category.

		
				
Given a Binary Search Tree and a target number, return true if there exist two elements in the BST
such that their sum is equal to the given target.

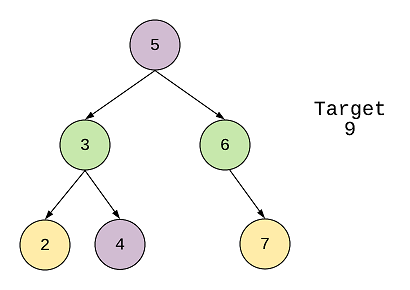
Example 1:
  
      Input: 
        5
       / \
      3   6
     / \   \
    2   4   7
    
    Target = 9
    
    Output: True

Example 2:

    Input: 
        5
       / \
      3   6
     / \   \
    2   4   7
    
    Target = 28
    
    Output: False

To solve this problem, we’ve to find a pair of numbers whose sum is equal to target. As the provided tree is binary search tree. We can check if an element exists in the tree in log₂ N time complexity.

So, the first solution that we’ll look into we’ll be based on that. In this solution, we’ll

Traverse through the BST
For every node, I’ll check if the element target - node.Value exists.
If it exists then I’ll return true
If it doesn’t then I’ll move to the next node and repeat the same process

Here is the code for that:

type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}

func findTarget(root *TreeNode, k int) bool {
	theRoot := root
	return preOrder(root, theRoot, k)
}

func preOrder(node, theRoot *TreeNode, k int) bool {
	if node == nil {
		return false
	}
	if (binarySearch(theRoot, node, k - node.Val)) {
		return true
	}
	return preOrder(node.Left, theRoot, k) || preOrder(node.Right, theRoot, k)
}

func binarySearch(root, nodeToIgnore *TreeNode, k int) bool {
	if root == nil {
		return false
	}
	if root.Val == k && root != nodeToIgnore {
		return true
	} else if root.Val > k {
		return binarySearch(root.Left, nodeToIgnore, k)
	} else {
		return binarySearch(root.Right, nodeToIgnore, k)
	}
}

In this approach, I’ve not used extra space and due to that the time complexity is O(n log₂ n). If we keep the values encountered during pre order traversal in a set then we won’t have to do the binary search for every node as we’ll be looking to the map this time.

type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}

var elementMap map[int]bool = make(map[int]bool)

func findTarget(root *TreeNode, k int) bool {
	if root == nil {
		return false
    }
    if _, ok := elementMap[k - root.Val]; ok {
        return true
    }
    elementMap[root.Val] = true
    return findTarget(root.Left, k) || findTarget(root.Right, k);
}

This time the time complexity is O(N), but the extra space complexity is O(N) as well.

This program is available here @ GitHub as well

Loading Comments... Disqus Loader

Two Sum IV - Input is a BST Solution - Leetcode

Leetcode Solution: Understand and solve Leetcode problem Two Sum IV - Input is a BST Solution(653)

Related Pages: